भाग-1 (part-1)
*जिसके हर के गुणनखंड में (एक भी 2 या 5 न हो) 3,7,11,.. आदि हो उसका दशमलव प्रसार आवर्ती और असांत(reccurring and non-terminating) होता है.
*जिसके हर के गुणनखंड में दोनों तरह की संख्याएं हो उसका दशमलव प्रसार आंशिक रूप से आवर्ती (partially reccurring)और आंशिक रूप से अनावर्ती, और असांत होता है.
* किसी भी भिन्न का दशमलव प्रसार असांत और पूर्णतः अनावर्ती नहीं हो सकता है.इस तरह के संख्या को अपरिमेय संख्या कहते है.
* 1/20, * 1/63, *1/6 * √2 ]
A. हर (denominator) के अंत में 9 हो: जैसे 1/19, 1/29, 148/149, 1998/1999, आदि
1/19 का दशमलव प्रसार करने के लिए --
➤ 19 में पूर्व अंक है '1', 1 का एकाधिक है 2 .
बाएं से दायें हल पाने के लिए (भाग विधि):
- 0. लिखने के बाद 1 को 2 से भाग देना है :भागफल(quotient) Q=0 और शेषफल(remainder) R=1 आएगा, इस 0 को दशमलव के बाद और 1 को इसी 0 के नीचे लिखेंगे .
- अगला भाज्य(next dividend)/N.D. है-- 10,इसको फिर 2 से भाग देना है: Q=5; R=0, इस 5 को 0.0 के बाद और 0 को इसी 5 के नीचे लिखेंगे.
- N.D. है-- 05 या 5,इसको 2 से भाग देने पर: Q=2 और R=1, इस 2 को 0.05 के बाद और 1 को इसी 2 के नीचे लिखेंगे.
- N.D. है-- 12, इसको 2 से भाग देने पर: Q= 6 और R=0, इस 6 को 0.052 के बाद और 0 को इसी 6 के नीचे.
- इस तरह से जारी रखेंगे 2 से भाग देना.
- --- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --
- --- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --
- अंत में आ जायेगा 1 और इससे आगे बढ़े तो फिर से सभी अंक दुहराने लगेंगे क्योंकि 1 से हमने सुरुआत किया था.
दायें से बाएं हल पाने के लिए (गुणा विधि):
- एकाधिक 2 है.
- दशमलव प्रसार में सबसे अंतिम आवर्ती(repeating) अंक 1 होगा(#क्यों ?- आगे बताएँगे)**.
- सबसे दायें में 1 लिखकर, उसे 2 से गुणा करेंगे, 1x2=2 इस 2 को 1 के बाएं (left) में लिखेगे.
- फिर 2 को 2 से गुणा करेंगे:2x2=4
- फिर 4x2=8 इस तरह हम पाते हैं--[ ...........................8421]
- फिर 8x2=16 अब होगा, [........................... 168421]
- फिर 6x2+1= 13 अब होगा, [.......................... 13168421
- फिर 3x2+1 =7 अब होगा, [.........................713168421]
- और इस तरह से तब तक गुणा करेंगे जब तक 1 पर न पहुँच जायें.हम 1 आने से ठीक पहले रुक जायेंगे.
- [.105126311151718914713168421] इससे आगे फिर 1 आ जायेगा.
जैसे : 1/19 में आख़िरी नौ है -- 947368421
+ 052631578--पहले के नौ अंक
--------------------
999999999
#क्यों ** 1 को मानक अंश(standard numerator) कहा जाता है. और यदि हर(deno.) के गुणनखंड में एक भी 2 या 5 न हो तो भिन्न का दशमलव प्रसार आवर्ती होता है. इस स्थिति में, यदि 1/(..a) = 0. ......b हो तो a.b = ..9 होता है.
जैसे-1/11 =0.09..0909.. ;1x9 =9
1/19= 0. ...........1.. ; 9x1 =9.
1/13= 0. ...........3.. ; 3x3 =9.
1/ 7= 0. ............7.. ;7x7 =49 अर्थात a और b के गुणनफल का अंतिम अंक 9 ही होगा.
* अगर मानक अंश वाले भिन्न का दशमलव प्रसार सांत हो तो a और b का गुणनफल का अंतिम अंक 0 होगा.
भाग विधि से (बाएं से दायें) कुछ और उदाहरण --
भाग विधि से (बाएं से दायें) कुछ और उदाहरण --
उदाहरण-1.
--इस उदाहरण में 1/49 का सहायक भिन्न (A.F.) 0.1/5 है क्योंकि 4 का एकाधिक 5 है.
- 0. लिखने के बाद 1 को 5 से भाग देंगे. तब Q=0 और R=1 मिलेगा.(इसे लिखेंगे-- 10).
- अगला भाज्य (N.D.) है: 10 =10, 10 को 5 से भाग देने पर Q=2 और R=0 मिलेगा.(इसे लिखेंगे--02)
- N.D. है: 02 = 2, इसे 5 से भाग देने पर Q=0 और R=2 मिलेगा.(इसे लिखंगे-- 20)
- N.D. है :20 इसे 5 से भाग देने पर Q=4 और R=0 मिलेगा.
- ------------------------------------------------------------
- --------------------------
उदाहरण-2.
उदाहरण-3.
ऊपर के उदाहरणों में अंश (Num.), हर(Deno.) से छोटा है. इस तरह के भिन्नों को उचित /सरल भिन्न(proper fraction) कहते हैं.
जब अंश (Num.), हर (Deno.) से बड़ा हो.
इस तरह के भिन्नों को विषम भिन्न (improper fraction) कहते हैं.
जैसे- 51/49
उदाहरण-1. 51/49; इसे 1+(2/49) लिखा जा सकता है.
इस तरह के भिन्नों को 1+ (2/49) लिख कर बना सकते हैं, और 2/49 को तो पहले की तरह हल करके उसे 1 के साथ जोड़ देंगे.
1+ 0.040816326....... = 1.0408163326.....
दूसरा तरीका : 51/49 के लिये सहायक भिन्न है 5.1/5
एक महत्वपूर्ण बात, 51>49 है,और स्पस्ट है की हमारा एकधिक अंक 5 होगा. अब सोचिये 51 को 5 से भाग देने पर दो अंक (Q=10) आ जायेंगे जो कि गलत होगा क्योंकि Q उतने ही अंकों के होने चाहिए जितने 9 हैं 'हर' (49) में. यदि 'हर' 199 हो तो Q में दो अंक होंगे और यदि 6999 हो तो Q में 3 अंक होंगे, ......... . अब एक नया शब्द आता है 'अवशेष अंक'. 5 से छोटे या बराबर अंक को 5 से भाग दे सकते हैं. अब जो 5 के बाद 1 है वही 1 अवशेष अंक है.
जब अंश (Num.), हर (Deno.) से बड़ा हो.
इस तरह के भिन्नों को विषम भिन्न (improper fraction) कहते हैं.
जैसे- 51/49
उदाहरण-1. 51/49; इसे 1+(2/49) लिखा जा सकता है.
इस तरह के भिन्नों को 1+ (2/49) लिख कर बना सकते हैं, और 2/49 को तो पहले की तरह हल करके उसे 1 के साथ जोड़ देंगे.
1+ 0.040816326....... = 1.0408163326.....
दूसरा तरीका : 51/49 के लिये सहायक भिन्न है 5.1/5
एक महत्वपूर्ण बात, 51>49 है,और स्पस्ट है की हमारा एकधिक अंक 5 होगा. अब सोचिये 51 को 5 से भाग देने पर दो अंक (Q=10) आ जायेंगे जो कि गलत होगा क्योंकि Q उतने ही अंकों के होने चाहिए जितने 9 हैं 'हर' (49) में. यदि 'हर' 199 हो तो Q में दो अंक होंगे और यदि 6999 हो तो Q में 3 अंक होंगे, ......... . अब एक नया शब्द आता है 'अवशेष अंक'. 5 से छोटे या बराबर अंक को 5 से भाग दे सकते हैं. अब जो 5 के बाद 1 है वही 1 अवशेष अंक है.
- 5 को 5 से भाग देंगे, Q=1 और R=0
- अगला भाज्य है 01 या 1, लेकिन 1 में 1 जोड़ना भी होगा.इस तरह वास्तविक भाज्य हुआ 2. 2 को 5 से भाग देने पर Q=0 और R=2.
- अगला वास्तविक भाज्य है:20 (यदि 5.1 में 1 के बाद कोई और अंक भी होता तो इस बार उसे जोड़ते) 20 को 5 से भाग देने पर Q=4, R=0.
- अब सारे कार्य पहले की ही तरह होंगे (जैसा कि 1/19,1/49 आदि में हमने किया).
- इसमें 89 को 17 से भाग देने पर,Q=5 और R=4 होगा.
- अगला भाज्य 45 +8 =53 होगा. इसे 17 से भाग देने पर,Q=3 और R=2.
- अगला भाज्य 23+7 =30. इसे 17 से भाग देने पर, Q=1 और R=13.
दशमलव(decimal) का स्थान स्वयं ही समझने का प्रयास करें. उदाहरण 3. में जब हम 7 पर पहुँचे थे उससे ठीक पहले दशमलव दिया गया है.और यह तरीका हर स्थान पर लागू होता है.
एक अन्य प्रकार --
यहाँ हम केवल उचित भिन्न (proper fraction) के दशमलव प्रसार की बात करेंगे.
यहाँ हम केवल उचित भिन्न (proper fraction) के दशमलव प्रसार की बात करेंगे.
कार्य विधि :
- 'हर'(Deno.) में सभी 9 के पहले जो अंक हैं उसे 'पूर्व' मानेंगे और उसी के एकाधिक से सहायक भिन्न बनायेंगे. जैसे-678/69999 का सहायक भिन्न है 0.0678/7.
- 'हर' में जितने 9 थे उतने अंकों के समूहों में एकाधिक से भाग देना होगा. जैसे-0678 में, चार-चार समूहों में 7 से भाग देंगे.
- 0678 में 7 से भाग दें तो, Q-समूह =0096 और R=6 होगा.
- अगला भाज्य-समूह है:60096 =60096, 7 से भाग देने पर Q-समूह =8585 और R=1 होगा.
- अगला भाज्य-समूह है:18585, 7 से भाग देने पर Q-समूह =2655 और R=0
- अगला भाज्य समूह होगा 02655 या 2655 जिसे 7 से भाग देने पर Q-समूह में तीन ही अंक मिलेंगे- 379 और शेष(R)=2. ध्यान दें कि हमें चार अंको के समूह चाहिए इसलिए 379 को 0379 लिखेंगे और तब उसके नीचे-बाएं में 2 लगायेंगे.
जैसे-60096 में R=6 है और Q-समूह का पहला अंक = 0. तो नियम के अनुसार 7 से पहले 60 को भाग देना है और 7x8=56; फिर 40 को 7से, 7x5=35; फिर 59 को 7 से, 7x8=56; फिर 36 को 7 से,7x5=35. और अंतिम भाग में जो शेष आया वह R है, R=1 (इसे लिखेंगे--18585).
इसी तरह 02655 में पहले 02 को 7 से भाग देंगे, 7x0=0 शेष =2; फिर 26 में 7 से, 7x3=21; फिर 55 में 7 से, 7x7=49; फिर 65 में 7 से, 7x9=63 और R=2.(इसे लिखेंगे-- 20379) *सबसे सुरुआत में R नहीं होता है तो पहले ही अंक को 7 से भाग देकर हम आगे बढ़े हैं.
- फिर अगला भाज्य समूह होगा 20379.
- .............................जितने अंक चाहिए उतना भाग देते जाईये.
ऊपर दो और उदाहरण दिए हैं उन्हें समझने का प्रयास करें.
B. 'हर' (denominator) के अंत में 8 हो: जैसे -1/18, 65/68, 1213/1998 आदि
भाग विधि (बाएं से दायें):
1/18 के दशमलव प्रसार पर विचार करते हैं--
'हर' (Deno.) में पूर्व अंक है '1' और 1 का एकाधिक होगा 2.
- A.F. 'हर' के अंतिम अंक पर निर्भर नहीं है यह तो 'पूर्व अंक' पर निर्भर होता है अर्थात जिन भिन्नों के हरों के पूर्व अंक एक जैसे होंगे उनके A.F. भी एक ही होंगे. किन्तु, बाद की क्रियाओं में अंतर है.
- 0. लिखने के बाद, 1 को 2 से भाग देने पर Q=0 और R=1 होगा.पहले की ही तरह 1 को 0 के नीचे लिखेंगे(RQ अर्थात 10).
- अगर 'हर' का अंतिम अंक 9 होता तो -- अगला भाज्य =10 =10 होता, लेकिन यहाँ 'हर' है 18 जिसका अंतिम अंक 8 (=9-1) है जो कि 9 से एक कम है , इसलिए अगला भाज्य के लिए 10 में Q गुणे 1 जोड़ना होगा. [RQ + Q.1]
- तब अगला भाज्य हुआ -- 10+0 =10
- इस 10 को 2 से भाग देने पर,Q=5 और R=0 , फिर से भागफल में 5 और उसके नीचे 0 लिख देंगे (05).
- अगला भाज्य होगा: 05 + 5 = 5+5 =10, फिर से 2 से भाग देने पर वही Q और R मिलेंगे और यह बार-बार होता रहेगा.
एक अन्य आवश्यक बात है जिसे एक और उदाहरण देकर हम समझायेंगे.-----
25/28 का दशमलव प्रसार करेंगे.
- सहायक भिन्न होगा --- 2.5/3
- 2.5 में 3 से भाग देने पर Q=8 और R=1 होगा (18).
- अगला भाज्य होगा- 18+8 =26
- 26 को 3 से 8 बार में नहीं बल्कि 8 से एक अधिक , 9 बार में भाग देंगे.इस तरह तो Q=9 मिला और R= -1 होगा [3x9+(-1) =26].
- अगला भाज्य होगा- [पहले 19 और -19 में अंतर समझ लें] -19+9 = -1+9=8.
- 8 को 3 से भाग देने पर,Q=2 और R=2.(इसे लिखेंगे 22).
- अगला भाज्य होगा- 22+2 =24 इसे 3 से भाग देने पर, Q=8 और R=0.(इसे लिखेंगे 08)
- अगला भाज्य होगा- 8+8=16,इसे 3 से भाग देने पर Q=5 और R=1.(इसे लिखेंगे 15)
- अगला भाज्य होगा 15+5=20, 3 से भाग देकर Q=7 और R= -1.
- -----------------------------------------------
- ---------------------------------
जब अंश > हर हो. (improper fraction के लिए)
135/28
यहाँ 'हर' है 28 जिसमें पूर्व अंक है- 2 और 2 का एकाधिक होगा 3.इसलिए 135/28 का दशमलव प्रसार करने के लिए सहायक भिन्न होगा: 13.5/3 .
इसमें अवशेष अंक है: 5 (याद कीजिये 51/49 जिसमें अवशेष अंक 1 था.)
135/28
यहाँ 'हर' है 28 जिसमें पूर्व अंक है- 2 और 2 का एकाधिक होगा 3.इसलिए 135/28 का दशमलव प्रसार करने के लिए सहायक भिन्न होगा: 13.5/3 .
इसमें अवशेष अंक है: 5 (याद कीजिये 51/49 जिसमें अवशेष अंक 1 था.)
- 13 को 3 से भाग देने पर, Q=4 और R=1; (इसे लिखेंगे-- 14).
- अगला भाज्य: 14+4 =14+4=18 और इसमें अवशेष अंक 5 जोड़ने पर, 18+5=23 होगा; 23 में 3 से भाग देने पर Q=8 और R= -1; (इसे लिखेंगे-- -18).
- अगला भाज्य: -18+8=(-10+8) +8=6 (यदि और भी अवशेष अंक होता तो उसे अभी जोड़ देते); 6 को 3 से भाग देने पर, Q=2 और R=0. (इसे लिखेंगे-- 02 )
- अगला भाज्य 02+2 =4, 3 से भाग देने पर, Q=1 और R=1 (इसे लिखेंगे-- 11)
- अगला भाज्य: 11+1 = 12, 3 से भाग देने पर, Q=4 और R=0.(इसे लिखेंगे-- 04).
- अगला भाज्य: 04+4 =8, 3से भाग देने पर, Q=2 और R=2.( इसे लिखेंगे-- 22).
- -----------------------------------------------------
- --- भाग देते जाइये , जितने अंकों तक दशमलव चाहिए उससे एक अधिक बार भाग दीजिये क्योंकि कभी कभी R ऋणात्मक भी लाना पड़ता है जैसे- यहाँ दुसरे step में हमने किया.
*हमने 'हर' के अंतिम अंक का '9 से 1 कम' होने के कारण से RQ के स्थान पर RQ + (Q गुणे 1) या RQ + Q को अगला भाज्य बनाया.
*इसे एक और तरीके से देख सकते हैं: (8 से अंत होने वाले) 'हर' का अंतिम अंक '10 से 2 कम' होगा इसलिए RQ के स्थान पर अगला भाज्य होगा: RQ + Q =(10R + Q) + Q =10R+2Q = R(2Q) या RQ'' .
जैसे:19 =>अगला भाज्य =28 [19'' =10+18=RQ''] या [(10+9)+9=RQ + Q]
एक और उदाहरण देखिये--
एक अन्य प्रकार
तीन आवश्यक बातें-
जब हर का अंतिम अंक 7 ,6,5,4,3,2,या 1 हो तब भिन्न का दशमलव प्रसार कैसे होगा जानने के लिए -------
वापस←
*इसे एक और तरीके से देख सकते हैं: (8 से अंत होने वाले) 'हर' का अंतिम अंक '10 से 2 कम' होगा इसलिए RQ के स्थान पर अगला भाज्य होगा: RQ + Q =(10R + Q) + Q =10R+2Q = R(2Q) या RQ'' .
जैसे:19 =>अगला भाज्य =28 [19'' =10+18=RQ''] या [(10+9)+9=RQ + Q]
एक और उदाहरण देखिये--
एक अन्य प्रकार
तीन आवश्यक बातें-
- 1698 को 1700 अनुमानित किया गया है इसलिए Q प्रत्येक बार दो और सिर्फ दो अंकों का होगा.
- पिछले बार की ही तरह, प्रत्येक बार अगला भाज्य RQ + Q या RQ'' होगा. जैसे- 1011 (Q=11, R=10) से अगला भाज्य मिलेगा: 1011 + 11=1022 ; या R22=1022=1022.
- कभी भी (अगला ) भाज्य 1700 या इससे अधिक नहीं होना चाहिए यदि ऐसा हुआ तो 17 से भाग देने पर Q तीन अंकों का आ जायेगा जो कि गलत होगा. ऐसी स्थिति में ऋणात्मक R प्राप्त करना चाहिए . जैसे- 968 में 17 से भाग देने पर,Q=56 और R=16 अब इसका अगला भाज्य का सोचिये वह तो 1656 + 56 =1712 इसलिए Q =57 कर दिया गया जिससे R= -1 मिला और साथ ही अगला भाज्य 14 हुआ.*
- दो लाइनों के बीच भाज्य लिखा गया है. पहला भाज्य 197 है, दूसरा भाज्य 1011 से 1022 मिला .......
- स्पष्ट है की दशमलव एक अंक के बाद होगा अर्थात 1.16018......
***आशा है आपको सब समझ में आ रहा होगा. यदि कोई कठिनाई हो रही हो तो comment करके बतायें. आप facebook page पर भी जाकर सवाल कर सकते हैं.
जब हर का अंतिम अंक 7 ,6,5,4,3,2,या 1 हो तब भिन्न का दशमलव प्रसार कैसे होगा जानने के लिए -------
वापस←







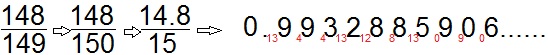



















1 टिप्पणी:
आपका वैदिक गणित के ऊपर यह ब्लॉग बहुत अच्छा है लेकिन समझने में फिर भी समस्या लग रही है।
वीडियो के माध्यम से वैदिक गणित समझाने की कृपा करें।
एक टिप्पणी भेजें