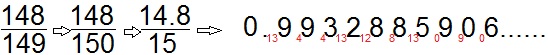(एकाधिकेन पूर्वेण + अन्त्ययोर्दशकेऽपि से) गुणा और वर्ग

अन्त्ययोर्दशकेऽपि के सहायता से संख्याओं का वर्ग और गुणा करना.

एकाधिकेन पूर्वेण से वर्ग: इस सूत्र के प्रयोग से 5 से अंत होने वाली संख्याओं का वर्ग किया जा सकता है.

जैसे: 35, 45, 65, 135, 125, 115 आदि का वर्ग.

35 का वर्ग

35 में 'पूर्व' अंक है 3 और 3 का एकाधिक होता है 4. इसलिए 35^2 =3x4\25 =1225

125 का वर्ग

125 में 'पूर्व' अंक है 12 और 12 का एकाधिक होता है 13. इसलिए 125^2 =12x13\25 =156\25 =15625

कुछ और उदाहरण--

1. 1995^2 =199x200\25 =39800\25 =3980025
2. 325^2 =32x33\25 =1056\25 =105625
3. 535^2 =53x54\25 =2862\25
4. 95^2 =9x10\25 =90\25 =9025.
5. 35^2 =3x4\25 =12\25 =1225.

अब किसी भी एक 5 से अंत होने वाली संख्या के वर्ग पर विचार कीजिये :

25^2 =25x25 --इसमें दोनों के 'पूर्व' अंक एक ही हैं और 'अंतिम' अंक 5 और 5 हैं अर्थात अंतिम' अंक का योग 10 है.

इस प्रकार यह नियम वैसे सभी संख्याओं पर भी लागू होता है जिनमें अंतिम अंको का योग 10 हो. इसके लिए एक उपसुत्र है -----------

'अन्त्ययोर्दशकेपि' का 'प्रयोग में' अर्थ है: अंतिम वाले का योग 10 हो या 10^n हो. n प्राकृत संख्या है.

अर्थात् 10 हो, या 100,1000, या 10000 या .....  हो.

जैसे- 56x54, 102x108,157x143 651x649 ,1998x1992,1998x1002  इत्यादि में, क्रमशः 6+4=10; 2+8=10; 57+43=100; 51+49=100; 8+2=10; 998+002=1000  है.

अब इनमें एक और बात पर ध्यान दीजिये,  1998x1992 में 'पूर्व' 199 है और 'अंतिम' में 8 और 2 है, जबकि 1998x1002 में 'पूर्व' 1 है और 'अंतिम' में 998 और 002 है. 

1998x1992 के गुणा पर विचार करें

दोनों के 'पूर्व' एक समान है  और 'अंतिम' (जो कि 8 और 2 है ) का योग 10 है. इसलिए उपरोक्त नियम इस पर काम कर जायेगा.

• 'पूर्व' को,  'पूर्व' के एकाधिक (एक-अधिक) से गुणा करेंगे. यहाँ पूर्व' है 1 और 199 का एकाधिक है 200 इसलिए 199x200=39800.
• 'अंतिम' है 8 और 2 (जिसका जोड़ =10). 8x2 करेंगे. और इससे मिलेगा 8x2=16.
• इस तरह से 1998x1992= 39800\16 =3980016.

1998x1002 के गुणा पर विचार करें

'पूर्व' है 1 और 'अंतिम' में है 998 और 002. 

• 1 को 1 के एकाधिक से गुणा करने पर, 1x2=2 मिलता है.
• अंतिम है 998और 002 (जिसका जोड़ है 1000). 998x002 =998x2 =(2000-4) =1996, किन्तु आधार 1000 है इसलिए अंतिम के गुणनफल से 6-अंक मिलना चाहिए यदि ऐसा नहीं होता है तो 0 की सहायता से 6-अंक पूरा करेंगे. इस तरह से 001996 मिला.
• अतः 1998x1002 =2\003996 =2001996.

कुछ और उदाहरण:

1. 54x56 =5x6\4x6 =30\24 =3024
2. 43x47 =4x5\3x7 =20\21 =2021
3. 119x111 =11x12\9x1 =132\09 =13209
4. 125x125 =12x13\5x5 =156\25 =15625.

यह आसान है यदि आपको नही लगता है तो --- गुणा के 'उर्ध्वतिर्यक' सूत्र का प्रयोग करें. 16 सूत्रों के साथ में हमने उर्ध्वतिर्यक का एक उदाहरण दिया है उसे समझने का प्रयास करें. यदि नहीं समझ पा रहे हों तो आप comment करके बतायें. आप हमारे facebook page पर भी सवाल कर सकते हैं साथ ही उस पर आपको 11 से गुणा करने की आसान विधि मिल जायेगी. 

एकाधिकेन पूर्वेण: भिन्नों को दशमलव में बदलने के लिए (2)

भाग-2 (part-2)

यह पोस्ट है   एकाधिकेन पूर्वेण >भिन्नों के दशमलव प्रसार >भाग-2. अगर आपने भाग-1 नहीं पढ़ा है तो पहले उसे ही पढ़िए.

C.  उन भिन्नों का दशमलव प्रसार जिनके हर(Denominator) का अंतिम अंक 7 हो

जैसे:- 1/17, 1/27, 1/37, 1/127, 324/327,  1/19997

1/137 = ?

• हर(Deno.) में पूर्व अंक है 13 जिसका एकाधिक होगा 4 इसलिए सहायक भिन्न होगा: 0.1/14
• आवश्यक बात  :  'हर' का अंतिम अंक है 7, जो कि 9 से दो कम है इसलिए प्रत्येक बार (अगला) भाज्य के लिए RQ + 2Q  या फिर ,7  10 से 3 कम है इसलिए RQ''' या R(3Q)

नोट:- 'अगला भाज्य' के लिए दोनों तरीके से कार्य करके दिखाया गया है.

• 0. लिखने के बाद 1 को 14 से भाग देने पर, Q=0 और R=1.     (इसे लिखेंगे 10)
• अगला भाज्य होगा 10; [RQ + 2Q = 10x1+2x0 या RQ'''=1(3x0)=10=10 ]
• 10 को 14 से भाग देने पर, Q = 0 और R =10.     (इसे लिखेंगे 100)
• अगला भाज्य होगा 10(3x0) =100=100; इसे 14 से भाग देने पर, Q=7 और R=2    (इसे लिखेंगे 27)
• अगला भाज्य होगा 2(3x7)=2(21)=10x2 +21 = 41   [याद कीजिये, RQ=10R+Q]   41 को 14 से भाग देने पर, Q=2 और R=13    (इसे लिखेंगे 132)
• अगला भाज्य होगा 132 + 2x2  =136   [RQ+2Q]; इसे 14 से भाग देने पर, Q=9 और R=10   (इसे लिखेंगे 109)
• अगला भाज्य होगा =127 [RQ'''] इसे 14 से भाग देने पर, Q=9 और R=1   (इसे लिखेंगे 19)
• अगला भाज्य होगा =37  .......

इस तरह से 1/137 = 0.00729927....

अब एक बात पर ध्यान दीजिये कि यदि 'हर' 17 या 27 या 37 या ... अर्थात पूर्व का अंक छोटा हो तो हर को 7 से गुणा करके हर का अंतिम अंक 9 बनाया जा सकता है लेकिन अंश(numerator) में भी 7 से गुणा करना पड़ेगा.

जैसे -   1/17 = 7/119  या 1/27 = 7/189.  हाँ पर इस तरह से 1/27=7/189 का पूर्व 18 बन जायेगा और उसका एकाधिक 19, मतलब कि 19 से प्रत्येक बार आपको भाग देना पड़ेगा (मुश्किल नहीं है).  और जब 'हर' का अंतिम अंक 9 हो तब तो आपको पता ही है कि कितना आसान है दशमलव प्रसार करना. (यदि नहीं पता है तो भाग 1 देखिये).




D.उन भिन्नों का दशमलव प्रसार जिनके 'हर'(Deno.) का अंतिम अंक 6 हो.

 जैसे:- 1/16, 25/26, 16585/19996 इत्यादि.

1/16 को हम लिख सकते हैं 3/48 और जब अंतिम अंक 8 हो तो दशमलव प्रसार कैसे करें यह भाग-1 में बताया गया है. 
इसी तरह से छोटे-छोटे हरों वाले भिन्न जिनके हरों के अंतिम अंक 6 हो उनमें 3 से गुणा कर उन्हें 8 से अंत होने वाले हरों ,वाले  भिन्नों  में बदला जा सकता है.


55/56 का दशमलव प्रसार करना है :

• सहायक भिन्न होगा: 5.5/6
• 0. लिखने के बाद 55 में 6 से भाग देने पर Q=9 और R= 1 (इसे लिखेंगे 19 ).
• अगला भाज्य होगा:46 [19 + 3x9 =46] या [19''''= 1(4x9) = 1x10+36 =46] और 46 को 6 से भाग देने पर Q=8 और R= -2 (इसे लिखेंगे -28)
• अगला भाज्य होगा: 12   [कैसे?]  इसे 6 से भाग देने पर, Q=2 और R=0 ( इसे लिखेंगे 02)
• फिर अगला भाज्य होगा: 8 [कैसे ?] इसे 6 से भाग देने पर, Q=1 और R=2 (इसे लिखेंगे 21)
• अगला भाज्य होगा: 24; 6 से भाग देने पर, Q=4 और R=0 (इसे लिखेंगे 04) 
• ---------------------------------------
• --------------
• जितने अंक चाहिए उतना भाग देते रहें.

इस तरह से 55/56 = 0.19 -28 02 21 04 .....होगा.

E. उन भिन्नों के दशमलव प्रसार जिनके 'हर' का अंतिम अंक 5 या 4,3,2,1 हो.

नोट:- यहाँ पर जो भी बताया जायेगा वह अधुरा होगा और जिसका शेष भाग आवर्ती दशमलव भिन्न वाले पोस्ट में लिखा जायेगा.

5 से अंत हो:

  जैसे- 24/25, 163/165, 1895/1331.

•  ऐसे भिन्नों के हरों में 5 से भाग देने पर हर के अंत में 1 या 3 या 5 या 7 या 9 आ जायेगा.
•  अंश में 5 से भाग दे कर आसानी से 1,3,7,या 9 वाले हरों से भिन्न में बदल सकते हैं 

और यदि फिर से 5 आ गया है तो एक और बार 5 से भाग दे दीजिये. (ऐसा न हो कि आप 125 से भाग देने का प्रयास कर रहे हों एकाधिकेन पूर्वेण से, इसके लिए तो आप अंश और हर में 8 से गुणा कर दें; इसी तरह के और भी उदाहरण हो सकते हैं जहाँ आपको 'एकाधिकेन' की आवश्यकता भी नहीं )

• 9 और 7 के लिए तो पता है ही आपको; 1 और 3 तीन के लिए अभी बताएँगे.

1 से अंत हो:

जैसे- 1/21, 1/121, 59/61, 19999/20001 इत्यादि

• इन भिन्नों के हरों में 9 से गुणा कर उसे 9 वाले, हरों वाले भिन्न में बदला जा सकता है.
• एक आवश्यक बात:  भिन्न के हर को 9 से गुणा कर 9 से अंत होने वाले भिन्न में बदलना हमेशा अच्छा नहीं है क्योंकि 'हर' बहुत ही बड़ा हो सकता है जिससे कठिनाई बढ़ जाएगी,  इसके लिए एकाधिकेन पूर्वेण सूत्र के बिना ही हल करने का एक आसान नियम है. इस नियम पर हम आवर्ती दशमलव भिन्न में चर्चा करेंगे.

• संक्षेप में नियम:------------------------------
• यदि भिन्न 19/21 हो तो सहायक भिन्न होगा: 19-1/20 => 18/20=> 1.8/2;
• RQ से अगला भाज्य R(9-Q) मिलेगा. इसका मतलब Q के 9 के पूरक को वास्तविक Q बनाना है.

जैसे RQ = 18 हो तो अगला भाज्य होगा: 11=11;  25 हो तो 24=24

2से अंत हो:

जैसे- 1/12, 21/32, 169/172 इत्यादि

इस तरह के भिन्नों के हरों के 4 से गुणा कर 8 से अंत होने वाले हरों में बदल सकते हैं.

• सीधे-सीधे बनाने के लिए भी नियम है जो अभी संक्षेप में बताया जा रहा है.
• सहायक भिन्न वही होगा जैसे 1-से अंत वाले में होता है.
• संक्षेप में:---  यदि अगला भाज्य RQ=18 हो वास्तविक भाज्य R(9-2Q) = 17 होगा.

3 से और 4 से अंत हो:

इनमे भी सहायक भिन्न वैसा ही होगा जैसा ऊपर के दोनों में बताया गया.

3 वाले में: RQ से R(9-3Q)   और   4 वाले में: RQ से R(9-4Q) .

बहुत ही जल्द आपको आवर्ती दशमलव भिन्न - पोस्ट मिल जायेगा.

अगर आपको समझने में कोई परेशानी हो रही हो तो comment करके बतायें या आप हमारे facebook page पर भी सवाल कर सकते हैं .

A.एकाधिकेन पूर्वेण सूत्र विस्तार से

एकाधिकेन पूर्वेण सूत्र

एकाधिकेन पूर्वेण सूत्र वैदिक गणित का पहला सूत्र है (यह सूत्र हर जगह पहले स्थान पर आपको मिलेगा  इसलिए हम भी इसी क्रम को मानकर यह पोस्ट और अन्य भी पोस्ट लिखेंगे ). यह सर्वाधिक उपयोग होने वाले सूत्रों में से एक है. 'एकाधिकेन' सूत्र की उपयोगिता गणित के कितने क्षेत्रों में है इस बात का आकलन करने से पहले यह भी जान लें कि स्वामी तीर्थ जी ने इस सूत्र पर पूरा का पूरा एक किताब लिखा था (ऐसा sources कहते हैं ; संभवतः उस हस्तलिपि का अस्तित्व अब नहीं है) . अतः वर्तमान में इस सूत्र के जितने प्रयोग प्रचलित हैं हम भी उन्हें ही पढ़ेंगे. 

कहाँ-कहाँ इस सूत्र का प्रयोग होता है :

1. भिन्नों को दशमलव में बदलने के लिए.[भाग-1] और [भाग-2]
2. 'अन्त्ययोर्दशकेऽपि' उपसूत्र की सहायता से संख्याओं का गुणा और वर्ग करने के लिए.
3. किसी संख्या का किसी अन्य संख्या से विभाज्यता का जाँच(divisibility test) करने के लिए.
4. आंशिक भिन्नों के प्रयोग से समाकलन(integration).

एकाधिकेन पूर्वेण --भिन्नों को दशमलव में बदलने के लिए (1)

भाग-1    (part-1)

[भिन्नों के संबंध में--

*जिसके हर (denominator) के गुणनखंड (factors) में केवल 2 या 5 हो ,उसका दशमलव प्रसार साधारण/ अनावर्ती और सांत(non-recurring and terminating) होता है.
*जिसके हर के गुणनखंड में (एक भी 2 या 5 न हो) 3,7,11,.. आदि हो उसका दशमलव प्रसार आवर्ती और असांत(reccurring and non-terminating) होता है.
*जिसके हर के गुणनखंड  में दोनों तरह की संख्याएं हो उसका दशमलव प्रसार आंशिक रूप से आवर्ती (partially reccurring)और आंशिक रूप से अनावर्ती, और असांत होता है.
* किसी भी भिन्न का दशमलव प्रसार असांत और पूर्णतः अनावर्ती  नहीं हो सकता है.इस तरह के संख्या को अपरिमेय संख्या कहते है.

* 1/20,                 * 1/63,                        *1/6                       * √2     ]

A. हर (denominator) के अंत में 9 हो: जैसे 1/19, 1/29, 148/149, 1998/1999, आदि

1/19 का दशमलव प्रसार करने के लिए -- 

➤ 19 में पूर्व अंक है '1', 1 का एकाधिक है 2 .

बाएं से दायें हल पाने के लिए (भाग विधि): 

• सहायक भिन्न (auxiliary fraction)/ A.F. होगा--->

•   0.   लिखने के बाद 1 को 2 से भाग देना है :भागफल(quotient) Q=0 और शेषफल(remainder) R=1 आएगा, इस 0 को दशमलव के बाद और 1 को इसी 0 के नीचे लिखेंगे .
   --    1 यहाँ 0 के उपसर्ग के रूप में है.
• अगला भाज्य(next dividend)/N.D. है-- 10,इसको फिर 2 से भाग देना है: Q=5; R=0, इस 5 को   0.0 के बाद और 0 को इसी 5 के नीचे लिखेंगे.
  
• N.D. है-- 05 या 5,इसको 2 से भाग देने पर: Q=2 और R=1, इस 2 को 0.05 के बाद और 1 को इसी 2 के नीचे लिखेंगे.
  
• N.D. है-- 12, इसको 2 से भाग देने पर: Q= 6 और R=0, इस 6 को 0.052 के बाद और 0 को इसी 6 के नीचे.
  
• इस तरह से जारी रखेंगे 2 से भाग देना.
• --- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --
• --- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --
• अंत में आ जायेगा 1 और इससे आगे बढ़े तो फिर से सभी अंक दुहराने लगेंगे क्योंकि 1 से हमने सुरुआत किया था.
   

यदि हम R=0 को प्रत्येक बार न भी लिखें तो कोई अंतर नहीं होता है.--

दायें से बाएं  हल पाने के लिए (गुणा विधि):

• एकाधिक 2 है.

• दशमलव प्रसार में सबसे अंतिम आवर्ती(repeating) अंक 1 होगा(#क्यों ?- आगे बताएँगे)**.

• सबसे दायें में 1 लिखकर, उसे 2 से गुणा करेंगे, 1x2=2 इस 2 को 1 के बाएं (left) में लिखेगे.

• फिर 2 को 2 से गुणा करेंगे:2x2=4

• फिर 4x2=8 इस तरह हम पाते हैं--[ ...........................8421]

• फिर 8x2=16 अब होगा,  [........................... 168421]

• फिर 6x2+1= 13 अब होगा,  [.......................... 13168421

• फिर 3x2+1 =7 अब होगा,  [.........................713168421]
• और इस तरह से तब तक गुणा करेंगे जब तक 1 पर न पहुँच जायें.हम 1 आने से ठीक पहले रुक जायेंगे.

•   [.105126311151718914713168421] इससे आगे फिर 1 आ जायेगा.
  ...

* एक अन्य विधि से हमारा कार्य आधा हो जाता है. हम जानते हैं की 1/19 के दशमलव प्रसार में आवर्ती अंकों (repeating digits) की संख्या (19-1=) 18 होती है. तब यदि पहले के नौ(nine) अंक पता हो तो आख़िरी के नौ अंक सीधे ही मिल जायेंगे और इसी तरह आख़िरी वाले पता हो पहले वाले मिल जायेंगे.

जैसे : 1/19 में आख़िरी नौ है -- 947368421

                                         +   052631578--पहले के नौ अंक

                                              --------------------

                                              999999999

#क्यों **  1 को मानक अंश(standard numerator) कहा जाता है. और यदि हर(deno.) के गुणनखंड में एक भी 2 या 5 न हो तो भिन्न का दशमलव प्रसार आवर्ती होता है.  इस स्थिति में, यदि 1/(..a) = 0. ......b हो तो a.b = ..9 होता है.

जैसे-1/11 =0.09..0909..  ;1x9 =9

        1/19= 0. ...........1.. ; 9x1 =9.

        1/13= 0. ...........3.. ; 3x3 =9.

        1/ 7= 0. ............7.. ;7x7 =49 अर्थात a और b के गुणनफल का अंतिम अंक 9 ही होगा.

* अगर मानक अंश वाले भिन्न का दशमलव प्रसार सांत हो तो a और b का गुणनफल का अंतिम अंक  0 होगा.

भाग विधि से (बाएं से दायें) कुछ और उदाहरण --

उदाहरण-1.

--इस उदाहरण में 1/49 का सहायक भिन्न (A.F.)  0.1/5 है  क्योंकि 4 का एकाधिक 5 है.

• 0. लिखने के बाद 1 को 5 से भाग देंगे. तब Q=0 और R=1 मिलेगा.(इसे लिखेंगे-- 10).

• अगला भाज्य (N.D.) है: 10 =10, 10 को 5 से भाग देने पर Q=2 और R=0 मिलेगा.(इसे लिखेंगे--02)  
• N.D. है: 02 = 2, इसे 5 से भाग देने पर Q=0 और R=2 मिलेगा.(इसे लिखंगे-- 20)
• N.D. है :20 इसे 5 से भाग देने पर Q=4 और R=0 मिलेगा.
• ------------------------------------------------------------
• --------------------------

और इस तरह से जितने अंक चाहिए उतना भाग करते जायेंगे.अंतिम आवर्ती अंक 1 आएगा इसके बाद भी भाग करते रहे तो फिर से 0204... आने लगेंगे.

उदाहरण-2.

उदाहरण-3.

ऊपर के उदाहरणों में अंश (Num.), हर(Deno.) से छोटा है. इस तरह के भिन्नों को उचित /सरल  भिन्न(proper fraction) कहते हैं.


जब अंश (Num.), हर (Deno.) से बड़ा हो.

इस तरह के भिन्नों को विषम भिन्न (improper fraction) कहते हैं.
जैसे-  51/49 
उदाहरण-1.  51/49;  इसे 1+(2/49) लिखा जा सकता है.
इस तरह के भिन्नों को 1+ (2/49) लिख कर बना सकते हैं, और 2/49 को तो पहले की तरह हल करके उसे 1 के साथ जोड़ देंगे.

1+ 0.040816326.......  = 1.0408163326.....

दूसरा तरीका : 51/49 के लिये सहायक भिन्न है 5.1/5

एक महत्वपूर्ण बात, 51>49 है,और  स्पस्ट है की हमारा एकधिक अंक 5 होगा. अब सोचिये 51 को 5 से भाग देने पर दो अंक (Q=10) आ जायेंगे जो कि गलत होगा क्योंकि Q उतने ही अंकों के होने चाहिए जितने 9 हैं 'हर' (49) में. यदि 'हर' 199 हो तो Q में दो अंक होंगे और यदि 6999 हो तो Q में 3 अंक होंगे, ......... . अब एक नया शब्द आता है 'अवशेष अंक'. 5 से छोटे या बराबर अंक को 5 से भाग दे सकते हैं. अब जो 5 के बाद 1 है वही 1 अवशेष अंक है.   

• 5 को 5 से भाग देंगे, Q=1 और R=0
• अगला भाज्य है 01 या 1, लेकिन 1 में 1 जोड़ना भी होगा.इस तरह वास्तविक भाज्य हुआ 2.   2 को 5 से भाग देने पर Q=0 और R=2.
• अगला वास्तविक भाज्य है:20 (यदि 5.1 में 1 के बाद कोई और अंक भी होता तो इस बार उसे जोड़ते) 20 को 5 से भाग देने पर Q=4, R=0.
• अब सारे कार्य पहले की ही तरह होंगे (जैसा कि 1/19,1/49 आदि में हमने  किया). 

उदाहरण-2.
  इसमें अवशेष अंक 3 और 2 हैं.

उदाहरण-3.
  इसमें अवशेष अंक 8 और 7 है.

• इसमें 89 को 17 से भाग देने पर,Q=5 और R=4 होगा.
• अगला भाज्य 45 +8 =53 होगा. इसे 17 से भाग देने पर,Q=3 और R=2.
• अगला भाज्य 23+7 =30. इसे 17 से भाग देने पर, Q=1 और R=13.

अगला भाज्य 131 है--अब पहले के तरह से भाग देते हुए, जितने अंकों तक दशमलव प्रसार चाहिए उतने भाग करते जाइये.

दशमलव(decimal) का स्थान स्वयं ही समझने का प्रयास करें. उदाहरण 3. में जब हम 7 पर पहुँचे थे उससे ठीक पहले दशमलव दिया गया है.और यह तरीका हर स्थान पर लागू होता है.

एक अन्य प्रकार --
यहाँ हम केवल उचित भिन्न (proper fraction) के दशमलव प्रसार की बात करेंगे.

विस्तार से देखें--

कार्य विधि : 

• 'हर'(Deno.) में सभी 9 के पहले जो अंक हैं उसे 'पूर्व' मानेंगे और उसी के एकाधिक से सहायक भिन्न बनायेंगे. जैसे-678/69999 का सहायक भिन्न है 0.0678/7.
• 'हर' में जितने 9 थे उतने अंकों के समूहों में एकाधिक से भाग देना होगा. जैसे-0678 में, चार-चार समूहों में 7 से भाग देंगे.
• 0678 में 7 से भाग दें तो, Q-समूह =0096 और R=6 होगा.
• अगला भाज्य-समूह है:60096 =60096, 7 से भाग देने पर Q-समूह =8585 और R=1 होगा.
• अगला भाज्य-समूह है:18585, 7 से भाग देने पर Q-समूह =2655 और R=0
• अगला भाज्य समूह होगा 02655 या 2655 जिसे 7 से भाग देने पर Q-समूह में तीन ही अंक मिलेंगे- 379 और शेष(R)=2. ध्यान दें कि हमें चार अंको के समूह चाहिए इसलिए 379 को 0379 लिखेंगे और तब उसके नीचे-बाएं में 2 लगायेंगे.

एक नियम मान लें तो सुविधा होगी: ये जो 4-अंकों का Q-समूह में 7 से भाग दिया जाता है, इसमें पहले अंक को R के साथ भाग देना अनिवार्य है.

जैसे-60096 में R=6 है और Q-समूह का पहला अंक = 0. तो नियम के अनुसार 7 से पहले 60 को भाग देना है और 7x8=56; फिर 40 को 7से, 7x5=35; फिर 59 को 7 से, 7x8=56; फिर 36 को 7 से,7x5=35. और अंतिम भाग में जो शेष आया वह R है, R=1 (इसे लिखेंगे--18585).

           इसी तरह 02655 में पहले 02 को 7 से भाग देंगे, 7x0=0 शेष =2; फिर 26 में 7 से, 7x3=21; फिर 55 में 7 से, 7x7=49; फिर 65 में 7 से, 7x9=63 और R=2.(इसे लिखेंगे-- 20379) *सबसे सुरुआत में R नहीं होता है तो पहले ही अंक को 7 से भाग देकर हम आगे बढ़े हैं.

• फिर अगला भाज्य समूह होगा 20379.
• .............................जितने अंक चाहिए उतना भाग देते जाईये.

ऊपर दो और उदाहरण दिए हैं उन्हें समझने का प्रयास करें.

B. 'हर' (denominator) के अंत में 8 हो: जैसे -1/18, 65/68, 1213/1998 आदि

भाग विधि (बाएं से दायें):

1/18 के दशमलव प्रसार पर विचार करते हैं--

'हर' (Deno.) में पूर्व अंक  है '1' और 1 का एकाधिक होगा 2. 

• सहायक भिन्न (A.F.) होगा-------->

ये क्या ? 1/19 में भी A.F. यही था.  अगर आपके मन में ये सवाल आया हो तो धैर्य रखें बहुत जल्दी अंतर पता चल जाएगा.

• A.F.  'हर' के अंतिम अंक पर निर्भर नहीं है  यह तो 'पूर्व अंक' पर निर्भर होता है अर्थात  जिन भिन्नों के हरों के पूर्व अंक एक जैसे होंगे उनके A.F. भी एक ही होंगे.  किन्तु, बाद की क्रियाओं में अंतर है.

• 0. लिखने के बाद, 1 को 2 से भाग देने पर Q=0 और R=1 होगा.पहले की ही तरह 1 को 0 के नीचे लिखेंगे(RQ अर्थात 10).
  
• अगर 'हर' का अंतिम अंक 9 होता तो -- अगला भाज्य =10 =10 होता, लेकिन यहाँ 'हर' है 18 जिसका अंतिम अंक 8 (=9-1) है जो कि 9 से एक कम है , इसलिए अगला भाज्य के लिए 10 में Q गुणे 1 जोड़ना होगा.          [RQ + Q.1]

• तब अगला भाज्य हुआ -- 10+0 =10

• इस 10 को 2 से भाग देने पर,Q=5 और R=0 , फिर से भागफल में 5 और उसके नीचे 0 लिख देंगे (05).
  
• अगला भाज्य होगा: 05 + 5 = 5+5 =10, फिर से 2 से भाग देने पर वही Q और R मिलेंगे और  यह बार-बार होता रहेगा.
  

एक अन्य आवश्यक बात है जिसे एक और उदाहरण देकर हम समझायेंगे.-----

25/28 का दशमलव प्रसार करेंगे.

• सहायक भिन्न होगा ---     2.5/3
• 2.5 में 3 से भाग देने पर Q=8 और R=1 होगा (18).
• अगला भाज्य होगा- 18+8 =26

26 को 3 से भाग देने पर Q=8 और R=2 होगा अर्थात RQ = 28 लेकिन अब इसके बाद वाले भाज्य पर विचार कीजिये  28 +8 =28+8=36.  ध्यान दें  36 को 3 से भाग देने पर Q में दो अंक मिलेंगे जो कि गलत है.

• 26 को 3 से 8 बार में नहीं बल्कि 8 से एक अधिक , 9 बार में भाग देंगे.इस तरह तो Q=9 मिला और R= -1 होगा [3x9+(-1) =26].
• अगला भाज्य होगा-  [पहले 19 और -19 में अंतर समझ लें]   -19+9 = -1+9=8.
  

• 8 को 3 से भाग देने पर,Q=2 और R=2.(इसे लिखेंगे  22).
• अगला भाज्य होगा-   22+2 =24 इसे 3 से भाग देने पर, Q=8 और R=0.(इसे लिखेंगे 08)
• अगला भाज्य होगा-  8+8=16,इसे 3 से भाग देने पर Q=5 और R=1.(इसे लिखेंगे 15)
• अगला भाज्य होगा 15+5=20, 3 से भाग देकर Q=7 और R= -1.
•   -----------------------------------------------
• ---------------------------------

जब अंश > हर हो.  (improper fraction के लिए)

135/28
यहाँ 'हर' है 28 जिसमें पूर्व अंक है- 2 और 2 का एकाधिक होगा 3.इसलिए 135/28  का दशमलव प्रसार करने के लिए सहायक भिन्न होगा: 13.5/3  .
इसमें अवशेष अंक है: 5 (याद कीजिये 51/49 जिसमें अवशेष अंक 1 था.)

•  13 को 3 से भाग देने पर, Q=4 और R=1; (इसे लिखेंगे-- 14).
• अगला भाज्य: 14+4 =14+4=18 और इसमें अवशेष अंक 5 जोड़ने पर, 18+5=23 होगा; 23 में 3 से भाग देने पर Q=8 और R= -1; (इसे लिखेंगे-- -18).
• अगला भाज्य:  -18+8=(-10+8) +8=6 (यदि और भी अवशेष अंक होता तो उसे अभी जोड़ देते); 6 को 3 से भाग देने पर, Q=2 और R=0.  (इसे लिखेंगे-- 02 )
• अगला भाज्य 02+2 =4, 3 से भाग देने पर, Q=1 और R=1 (इसे लिखेंगे-- 11)
• अगला भाज्य: 11+1 = 12, 3 से भाग देने पर, Q=4 और R=0.(इसे लिखेंगे-- 04).
• अगला भाज्य: 04+4 =8, 3से भाग देने पर, Q=2 और R=2.( इसे लिखेंगे-- 22).
• -----------------------------------------------------
• --- भाग देते जाइये , जितने अंकों तक दशमलव चाहिए उससे एक अधिक बार भाग दीजिये क्योंकि कभी कभी R ऋणात्मक भी लाना पड़ता है जैसे- यहाँ दुसरे step में हमने किया.

*हमने 'हर' के अंतिम अंक का '9 से 1 कम' होने के कारण से RQ के स्थान पर RQ + (Q गुणे 1) या RQ + Q को अगला भाज्य बनाया.
*इसे एक और तरीके से देख सकते हैं: (8 से अंत होने वाले) 'हर' का  अंतिम अंक '10 से 2 कम' होगा इसलिए RQ के स्थान पर अगला भाज्य होगा: RQ + Q  =(10R + Q) + Q =10R+2Q = R(2Q) या RQ''  .
जैसे:19 =>अगला भाज्य =28   [19'' =10+18=RQ''] या   [(10+9)+9=RQ + Q]    

एक और उदाहरण देखिये--

एक अन्य प्रकार

तीन आवश्यक बातें-

1. 1698 को 1700 अनुमानित किया गया है इसलिए Q प्रत्येक बार दो और सिर्फ दो अंकों का होगा.
2. पिछले बार की ही तरह, प्रत्येक बार अगला भाज्य RQ + Q या RQ'' होगा. जैसे-  1011 (Q=11, R=10) से अगला भाज्य मिलेगा: 1011 + 11=1022 ;  या R22=1022=1022.
3. कभी भी (अगला ) भाज्य 1700 या इससे अधिक नहीं होना चाहिए यदि ऐसा हुआ तो  17 से भाग देने पर Q तीन अंकों का आ जायेगा जो कि गलत होगा. ऐसी स्थिति में ऋणात्मक R प्राप्त करना चाहिए . जैसे- 968 में 17 से भाग देने पर,Q=56 और R=16 अब इसका अगला भाज्य का सोचिये  वह तो 1656 + 56 =1712  इसलिए Q =57 कर दिया गया जिससे R= -1 मिला और साथ ही अगला भाज्य 14 हुआ.*

*14 को Q=00 और R=14 किया गया.

• दो लाइनों के बीच भाज्य लिखा गया है. पहला भाज्य 197 है, दूसरा भाज्य 1011 से 1022  मिला .......
• स्पष्ट है की दशमलव एक अंक के बाद होगा अर्थात 1.16018......

***आशा है आपको सब समझ में आ रहा होगा. यदि कोई कठिनाई हो रही हो तो comment करके बतायें.  आप facebook page पर भी जाकर सवाल कर सकते हैं.

जब हर का अंतिम अंक 7 ,6,5,4,3,2,या 1 हो तब भिन्न का दशमलव प्रसार कैसे होगा जानने के लिए -------    

→भाग-2  (part-2)

वापस←